اصول و کاربرد آنتروپومتری
اصول و کاربرد آنتروپومتری
اصول و کاربرد آنتروپومتری
Principles and Applications of anthropometry
در بعضی شرایط فضای کار و تجهیزات منحصرا مختص یک استفاده کننده معین طراحی می شود. سفارش لباس به خیاط, مدل لباس های زنانه و صندلی اتومبیل های مسابقه ای مواردی از این دست هستند. این قبیل وسایل را می توان جزء وسایل تجملی محسوب کرد. اکثر ما اماده هستیم تا راه حلهای شانسی و غیر علمی را تا حدی مطابق ویژگی های فیزیکی مان باشد بپذیریم. این امر ما را برای صرف هزینه بیشتر جهت دست یابی به تناسب کامل بی رغبت نموده است (حتی اگر فرض می کردیم که تناسب کامل در عمل قابل دسترسی است). زمانی که برای برخورداری از وجود مستقل ناچار باشیم طراحی تجملی و سفارشی برای تعداد کمی از ما ضرورت پیدا می کند: ویژگی های فیزیکی و احتیاجات افرادی که دارای معلولیت شدید هستند همچنان متغییر است که وسایل کمکی برای قابلیت تحرک و استقلال این افراد بایستی با توجه به این متغیرها و به طور فردی در نظر گرفته شود.
همه ما ضرورت تولید لباسهای زیر در اندازه های مختلف را می دانیم, اما ایا این درست است که مثلا بگوییم میز ها و صندلی ها نیز بایستی در اندازه ها و سایزها مختلف تولید شوند؟ جواب این است «بله, ام فقط در یک گسترده محدود». ما انتظار نداریم کخ خردسالان و بزرگسالان در دفاتر و مدارس از میزهای تحریر یکسان با اندازه های برابر استفاده کنید, اگرچه به نظر می رسد که با مشکل یکسان بودن میز شام در خانه کاملا خود گرفته اند. همچنین ما معمولا صندلیهای قابل تنظیم در اختیار ماشین نویسان قرار می دهیم, اما میزهای آنها عموما دارای ارتفاع ثابت می باشد.
واضح است که عدم تناسب میز و صندلی را راحت تر از عدم تناسب لباس و شلوار می پذیریم. آنچه کمتر مشهود است این است که چطور بهترین ابعاد را برای وسایل و تجهیزاتی که توسط تعداد زیادی از استفاده کنندگان مورد استفاده قرار می گیرند انتخاب کنیم و در چه مرحله ای بایستی نتیجه گرفت که قابلیت تنظیم و تغییر ضرورت دارد. برای حصول بهترین نتیجه و اتخاذ مناسبترین تصمیمات به سه دسته اطلاعات نیاز داریم:
- خصوصیات آنتروپومیتریکی جامعه استفاده کننده
- طریقی که این ویژگی ها ممکن است محدودیت هایی را بر طراحی تحمیل کند.
- ملاکهایی که تناسب موثر بین محصول و استفاده کننده را تعریف می کند.
قبل از بحث بیشتر در این زمینه, لازم است پایه و اساس کمی را که بحث ما بر آن متکی است بنا نهاده شود. سعی کرده ام که این عمل را با حداقل استفاده از معادلات ریاضی انجام دهم, این مقدار برای خوانندگان معمولی کافی است, متخصصین برای کسب جزئیات بیشتر می توانند به بخش 7-2 مراجعه کنند.
2-1- توصیف آماری تنوع اندازه های انسان
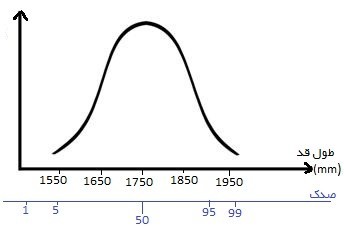
به منظور بنا نهادن مفاهیم آماری که تنوع اندازه های انسان را شرح می دهند, بیایید آزمایشی را انجام دهیم که نویسندگان علمی پیشین لابد آزمایش تخیل می نامیدند. فرض کنید در ساختمان عمومی بزرگی قرار دارید که افراد زیادی که نماینده جمعیت هستند در ان تردد دارند. دوست همراه شما که قمارباز حرفه ای است پیشنهاد می کند که بر روی اولین مردی که از انتها کریدور خواهد آمد شرط بندی کنید. (می توانستیم بر روی زنان, کودکان و یا هر شخص دیگر شرط بندی کنیم اما برای سهولت امر از نظر ریاضی تنها یک جنس از افراد بزرگسال را انتخاب کردیم). به فرض اینکه هیچ گونه اطلاع قبلی از افرادی که در آن حوالی تردد می کنند نداشته باشید. بر روی چه طول قدی شرط بندی خواهید کرد؟ شما احتمالا طول قدی را انتخاب میکنید که تقریبا نزدیک به میانگین باشد,زیرا تجربه به شما ثابت کرده است که افرادی با اندازه های متوسط معمولا بیشترند در حالی که افراد قد بلند و قد کوتاه, در مقایسه کمتر یافت می شوند. شما در واقع قضاوتی براساس احتمال نسبی وجود افراد یا طول قد های متفاوت و یا فراوانی نسبی که این افراد به طور تصادفی دارند, انجام داده اید. افراد میانگین محتمل تر از افرادی هستند که در حد پایین و بالا قرار می گیرند. و از این روست که شما بیشتر با آنها مواجه می شوید. شخصی که این شرط بندی به او پیشنهاد شده و دارای طرز تفکر آماری است می تواند شانس پیروزی خود را با اندازه گرفتن تمام مردانی که در آن ساختمان یافت می شوند, افزایش دهید. با اطلاعات به دست آمده می توان نموداری را رسم نمود, نظیر آنچه که در شکل 1-2 نمیش داده شده است و در آن احتمال فراوانی در محور عمودی و قد در محور افقی قرار گرفته است. منحنی که در این نمودار مشاهده می کنید به نام چگالی احتمال یا توزیع فراوانی شناخته می شود.
شکل 1-2: توزیع فراوانی (تابع چگالی احتمال) طول قد مردان بزرگسال انگلیسی, این مثالی از توزیع نرمال با توزیع گوسی است. مرجع اطلاعات نایت (1984)
منحنی خاصی که در اینجا رسم کرده ایم در اطراف نقطه اوج بهطور قرینه گسترده شده است. طول قد متوسط, یا به عبارتی میانگین, متحمل ترین طول قد است. از آنجا که این منحنی قرینه است, 50 درصد جمعیت کوتاهتر از مقدار متوسط و 50 درصد بلندترند, بنابراین می توان گفت که در این تابع میانگین معادل صدک پنجاهم می باشد. به طور کلی ان درصد (n%) افراد, کوتاهتر از صدک ان ام هستند. همچنین جایی در نزدیکی انتهای سمت چپ کحور افقی نقطه ای وجود دارد که می توان گفت «دقیقا 5 درصد از افراد کوتاهتراز ان داشته باشد». به طریق مشابه, با یک فاصله مساوی از میانگیت تا سمت راست نمودار به نقطه ای برمی خوریم که به ان صدک 95 شناخته می شود, نقطه ای که تنها 5 درصد از افراد بلندتر از آن هستند.ازنظر طول قد 90 درصد جمعیت بین صدکهای پنجم و نود پنجم قرار دارند. اما همین موضوع در مورد صدک های دوم و نود دوم یا سوم و نود سوم نیز صدق میکند. توجه به این نکته اهمیت دارد که با در نظرگرفتن خاصیت قرینه ای در حول میانگین, صدک های پنجم و نود و پنجم کوتاه ترین فاصله را در طول محور افقی مشخص می کنند که 90% از جمعیت را دربرمی گیرد. هنگام بحث در مورد صدکها دو نکته دیگر بایستی مورد توجه قرار گیرد. اول اینکه صدکها مختص جمعیتی هستند که توصیف می کنند, از این رو صدم نودم و پنجاهم قد برای جمعیت عمومی ممکناست معادل صدک هفتادم گروه شغلی خاصی نظیر افراد پلیس ویاشاید برابر با صدک پنجم جامعه بسکتبالیستهای حرفه ای باشد. دوم, صدک خاصی در طول قد می باشد امکان دارد دارای همان صدک در اندازه پهنای شانه یا پیرامون کمر باشد یا نباشد زیرا افراد در شکل و اندازه متفاوتند.
توزیع فراوانی که در شکل 1-2 نشان داده شده است (با منحنی ناقوسی شکل و ویژگی قرینه ای خود) در بیولوژی به طور اعم و در آنتروپومتری به طور اخص بسیار متداول و مرسوم است. این توزیع عموما به عنوان توزیع طبیعی شناخته می شود. البته نبایستی از این نام چنین استنتاج کرد که این توزیع به طریقی با افراد طبیعی با مفهومی از آن که در مقابل افراد غیر طبیعی قرار می گیرد, ارتباط دارد. بایستی به مفهومی توجه کنیم که چیزی شبیه به «توزیعی که آن را در مسائل علمی سودمندترین می یابیم» در ذهن ما تداعی شود.برای اجتاب از اشتباه, تعدادی از آمارگیران ترجیح می دهند که آن را توزیع گوسی بنامند. به نام ریاضیدان و فیزیکدان آلمانی یوهان گوس (1855-1777) که آنرا (در مبحث اشتباهات تصادفی در اندازه گیری کمیات فیزیکی) تشریح کرد. در مورد متغیری نظیر طول قد در کل جمعیت اگر بخواهیم چگونگی وراثت از یک نسل به نسل دیگر را مطالعه کنیم, امکان پیشگویی طبیعی بودن ان وجود دارد (به کتاب های ژنتیک مراجعه کنید). در واقع عملا واقعیت دارد که اکثر متغیرهای آنتروپومتریکی تا حد زیادی با توزیع طبیعی مطابقت دارد (حداقل در جمعیتهای همگن).
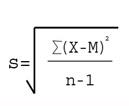
این یک حالت راحت و مطلوب مساله است زیرا توزیع طبیعی را می توان به وسیله یک معادله نسبتا ساده ریاضی توصیف کرد. فرم واقعی این معادله نبایستی موجوب نگرانی ما شود زیرا استفاده از آن درعمل کمتر محتمل است. نکته با اهمیت این است که این معادله تنها دارای دو پارامتر است. (در ریاضیات پارامتر کمیتی است که در مورد خاص ثابت بوده اما موارد مختلف متغییر است). یکی از این پارامترها میانگین است. میانگین, محل توزیع فراوانی را در روی محور افقی مشخص می کند. پارامتر دیگر کمیتی است به نام انجراف معیار استاندارد (S) که شاخصی از درجه پراکندگی در جمعیت مورد نظر می باشد, برای مثال پهنای توزیع یا حدی که مقدار منفرد در اطراف میانگین پراکنده هستند یا از آن انحراف دارند را مشخص می کند. مثلا اگر می خواستیم جامعه کل مردان و جامعه پرسنل نیروی پلیس را با یکدیگر مقایسه کنیم در میابیم که میانگین در جامعه ی پرسنل پلیس بیشتر و انحراف استاندارد کوچکتر می باشد؛ زیرا به طور متوسط افراد پلیس نسبت به بقیه دارای قد بلندتری بوده و گوناگونی طول قد در آنها نیز کمتر است. انحراف استاندارد (S) نمونه ای از افراد از یک جکعیت انتخاب شده اند با معادله زیر بدست می آید:
(2-1)
که در آن M میانگین متغیر مورد نظر, X مقدار متغیر مورد نظر و n تعداد نمونه است. ( با استفادهاز n-1 در معادله تورش ناشی از محدود بودن تعداد نمونه صحیح شده, پیشگویی بهتری از انحراف استاندارد به عمل می آید.)
یک توزیع طبیعی کاملا به وسیله میانگین و انحراف استاندارد خود تعریق می شود. اگر این دو پارامتر مشخص باشند امکان محاسبه هر صدکی بدون مراجعه به اطلاعات خام (برای مثال اطلاعات مروبط هب اندازه گیری هها از افراد جمعیت) وجود دارد. صدک پی ام یک متغیر با معادله زیر به دست می آید.
z برای صدک مورد نظر مقداری ثابت است که از جدول آماری به دست می آید. دسته ای از مقادیر P و Z در جدول 1-2 ارائه شده است. فرض کنید قصد داریم صدک نودم طول قد مردان بزرگسال انگلیسی را محاسبه کنیم. میانگین طول قد مردان انگلیسی برابر با 1740 میلی متر و انحراف استاندارد 70 میلی متر است (رجوع کنید به جدول 1-4). از جدول 1-2 می توان دید که وقتی P=90 باشد, Z برابر با 1.28 خواهد بود.
بنابر این مقدار صدک نودم طول قد برابر است با:
1740+70 × 1.28=1824 میلی متر
همین طور ممکن است بخواهیم محاسبه را بهطور معکوس انجام دهیم و مقدار صدک را برای طول قد معینی به دست آوریم. طول قد 1625 میلی متر به اندازه 1.64 انحراف استاندارد کمتراز مقدار میانگین است (S×1.64). یعنی Z برابر 1.64- خواهد بود.
با استفاده از جدول 1-2 می توان دریافت که مقدار مذکور معادل صدک پنجم می باشد.
در اینجا برای حفظ ایجاز در توصیف پارامترهای توزیع طبیعی از علایم قرار دادی استفاده می کنیم. هر گاه عددی با علامت کروشه [ ] به دنبال عدد دیگری آمد بدان معنی است که عدد اول میانگین و عدد داخل کروشه انحراف استاندارد آن می باشد. بنابراین, «عبارت طول قد مردان انگلیسی [70]1740 میلی متر است» یعنی « طول قد مردان انگلیسی دارای توزیعی طبیعی با میانگین 1740 میلی متر و انحراف استاندارد 70 میلی متر می باشد.
جدول 1-2: مقادیر P و Z توزیع طبیعی
| Z | P | Z | P | Z | P | Z | P |
| 0.71 | 76 | 0.03 | 51 | -0.64 | 26 | -2.33 | 1 |
| 0.74 | 77 | 0.05 | 52 | -0.61 | 27 | -2.05 | 2 |
| 0.77 | 78 | 0.08 | 53 | -0.58 | 28 | -1.88 | 3 |
| 0.81 | 79 | 0.10 | 54 | -0.55 | 29 | -1.75 | 4 |
| 0.84 | 80 | 0.13 | 55 | -0.52 | 30 | -1.64 | 5 |
| 0.88 | 81 | 0.15 | 56 | -0.50 | 31 | -1.55 | 6 |
| 0.92 | 82 | 0.18 | 57 | -0.47 | 32 | -1.48 | 7 |
| 0.95 | 83 | 0.20 | 58 | -0.44 | 33 | -1.41 | 8 |
| 0.99 | 84 | 0.23 | 59 | -0.41 | 34 | -1.34 | 9 |
| 1.04 | 85 | 0.25 | 60 | -0.39 | 35 | -1.28 | 10 |
| 1.08 | 86 | 0.28 | 61 | -0.36 | 36 | -1.23 | 11 |
| 1.13 | 87 | 0.31 | 62 | -0.33 | 37 | -1.18 | 12 |
| 1.18 | 88 | 0.33 | 63 | -0.31 | 38 | -1.13 | 13 |
| 1.23 | 89 | 0.36 | 64 | -0.28 | 39 | -1.08 | 14 |
| 1.28 | 90 | 0.39 | 65 | -0.25 | 40 | -1.04 | 15 |
| 1.34 | 91 | 0.41 | 66 | -0.23 | 41 | -0.99 | 16 |
| 1.41 | 92 | 0.44 | 67 | -0.20 | 42 | -0.95 | 17 |
| 1.48 | 93 | 0.47 | 68 | -0.18 | 43 | -0.92 | 18 |
| 1.55 | 94 | 0.50 | 69 | -0.15 | 44 | -0.88 | 19 |
| 1.64 | 95 | 0.52 | 70 | -0.13 | 45 | -0.84 | 20 |
| 1.75 | 96 | 0.55 | 71 | -0.10 | 46 | -0.81 | 21 |
| 1.88 | 97 | 0.58 | 72 | -0.08 | 47 | -0.77 | 22 |
| 2.05 | 98 | 0.61 | 73 | -0.05 | 48 | -0.74 | 23 |
| 2.33 | 99 | 0.64 | 74 | -0.03 | 49 | -0.71 | 24 |
| 0.67 | 75 | 0 | 50 | -0.67 | 25 | ||
|
Z |
P |
Z |
P |
|
1.96 |
97.5 | -1.96 | 2.5 |
| 2.58 | 99.5 | -2.58 | 0.5 |
| 3.09 | 99.9 | -3/09 | 0.1 |
| 3.72 | 99.99 | -3.72 | 0.01 |
| 5.26 | 99.999 | -4.26 | 0.001 |
استاندارد 70 میلی متر می باشد» ( این یک قرارداد کاملا فرضی است که در خارج از این کتاب مصداق ندارد). [ همچنین توجه داشته باشید که مثلا ILe 95% یعنی صدک نود و پنجم]
اکثر ابعاد خطی بدن دارای توزیع طبیعی هستندو این موضوع قطعا مساله را برای استفاده کنندگان اطلاعات آنتروپومتریکی سهل تر می سازد. البته انواع دیگری از توزیع فراوانی وجود دارد که گاهی در آنتروپومتری عملی مطرح می شوند.
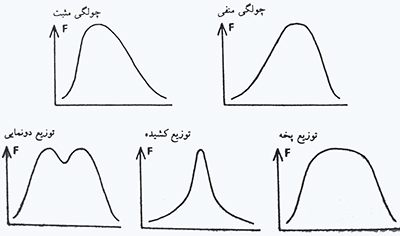
توزیع های دیگری نیز وجود دارند که در شکل 2-2 نماش داده شده اند.
شکل 2-2: انحراف از حالت طبیعی در توزیع های آماری داده های آنتروپومتریکی
در اغلب جمعیتها, وزن بدن و قدرت عضلانی چولگی مثبت نشان میدهند. به نظر می رسد که نسبت نامتناسبی از افراد سنگین وزن و قوی و افراد سبک وزن و ضعیف در جامعه وجود داشته باشد به طوری که تعداد افراد سنگین و قوی بیشتر از افراد سبک و ضعیف است.از طرف دیگر ادغام دو توزیع طبیعی نظیر مردان و زنان یا بزرگسالان و کودکان توزیع جدیدی را به دست می دهد که توزیع پخه و یا حتی توزیع دو نمایی (توزیعی که دارای دو نقطه زوج است) می باشد. اگر با این فرض اشتباه پیش برویم که این توزیع ها همانند توزیع طبیعی هستند و صدکها را براساس فرمول یاد شده محاسبه کنیم, چه اتفاقی خواهد افتاد؟ اشتباهاتی رخ خواهد داد که بزرگی آنها بر مبنای میزان انحراف از حالت طبیعی در توزیع جمعیت تعیین می شود. در بسیاری از شرایط اشتباهات قابل چشم پوشی هستند. تلفیق اطلاعات مربوط به زنان و مردان نکته مورد نظر است. از نقطه نظر تئوری, بر آیند حاصل از ادغام دو توزیع که حال به صورت تک جنسی در آمده است دارای توزیع پخه است.
انحراف از حالت طبیعی در عمل آن قدر ناچیز هستند که می توان از آنها چشم پوشی کرد. تنها طریق دیگر که از فرض طبیعی بودن توزیع اجتناب می ورزد این است که صدکها مستقیما با شمارش تعداد ستون ها در نمودار ستونی محاسبه می شوند اما از انجا که استفاده از این طریق مستلزم وجود نمونه ای با حجم زیاد است, به ندرت امکان پذیر بوده و در مقالات نیز تعداد بسیار ناچیزی از دسته های اطلاعاتی با این درجه از دقت و صحت بنا گذاشته شده اند. به طور کلی بهترین راه حل این است که فرض کنیم توزیع حاصل طبیعی است اما در مواردی که این فرض مورد تردید قرار می گیرد بایستی با دقت و ملاحظه کاری با آن برخورد کرد. از این به بعد, بحث ما عمدتا بر روی توزیع های طبیعی متمرکز و محدود می شود.
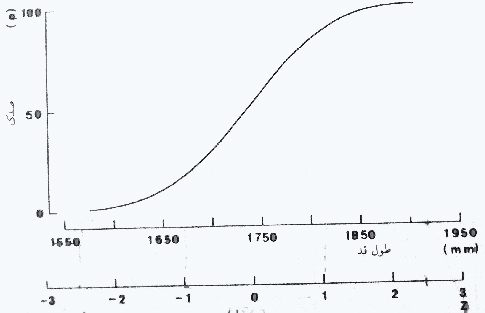
برای پاره ای از مقاصد ممکن است رسم منحنی توزیع طبیعی, بع شکل طبیعی مفیدتر باش و اطلاعات بیشتری را در اختیار بگذارد. در این صورت صدک ها در مقابل مقادیر بعد مورد نظر رسم می شوند (یا اگر محور افقی براساس انحراف استاندارد طبقه بندی شده باشد نموداری خواهیم داشت که در آن P در محور عمودی و Z در محور افقی قرار دارد). منحنی بدست آمده تحت عنوان منحنی نرما اُجیو شناخته می شود (به شمل 3-2 نگاه کنید) مزیت چنین نموداری این است که امکان خواندن مستقیم صدکها را قادر می سازد تا نتیجه در نظر گرفتن درصدی از جمعیت را که در محدوده طراحی قرار می گیرند مورد ارزیابی قرار دهیم. در یک مثال ساده شکل 3-2 مستقیما درصدی از مردان انگلیسی را مشخص می کند که می توانند بدون خمم شدن و یا مجروح کردن خود از زیر یک مانع هوایی با ارتفاع معین عبور کنند.
شکل 3-2: توزیع فراوانی قد مردان انگلیسی, به صورت تجمعی
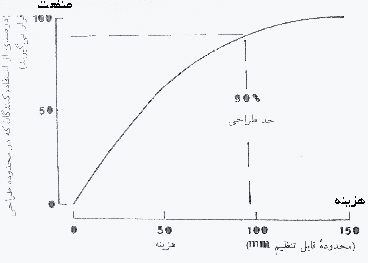
نموار تجمعی در ناحیه میانگین (یعنی نقطه ای که حداکثر احتمال وجود دارد) بیشترین شیب را دارد و به طرف انتهای بالایی منحنی, به طور ثابت از شیب آن کاسته می شود. منحنی در نقاط صفر و صددرصد به صورت مجانب با خط افقی در می آید (در تئوری این خطوط یکدیگر را در بی نهایت قطع می کنند). به همین دلیل در طراحی در نظر گرفتن صدکهای حد بالایی و پایینی بسیار مشکل است (در شکل 1-2 به این مسئله اشاره شد که صدکها در مرکز متراکم بوده و در حدود نهایی گسترده و پراکنده هستند). نتیجه عملی این مطلب این است که هر درصد مطلوبی از جمعیت که مایل باشیم در محدوده طراحی قرار دهیم, محدودیتهایی را در طراحی ایجاد خواهد کرد. در بحث هزینه /منفعت در شرایطی قرار داریم که سود برگشتی به طور ثابت کاهش می یابد. شکل 4-2 این مساله را با توجه به قابلیت تنظیم ارتفاع نشیمنگاه صندلی نشان می دهد. محاسبات براساس معیاری صورت گرفته اند که در آن ارتفاع فوق بایستی برابر با «ارتفاع رکبی» باشد که در آن توزیع تک جنسی مردان و زنان انگلیسی برابر [30] 445 میلی متر می باشد.
حال چگونه بایستی این خط را رسم کرد تا در فرایند طراحی کلیه افرادی که حتی در حدود نهایی هستند مورد توجه قرار گیرند؟ برای این سوال پاسخ منفردی وجود ندارد. یک راه حل کاملا اختیاری که در بساری از موارد مناسب تشخیص داده شده است طراحی برای محدوده بین صدکهای پنجم و نود و پنجم است, یعنی 90% از بخش میانه جمعیت.
شکل 4-2: تابع هزینه/منفعت آنتروپومتریکی که درصدی از افراد جمعیت هدف را نشان می دهد که به وسیله گشترده ای از ارتفاع های مختلف یک صندلی قابل تنظیم, در محدود طراحی قرار گرفته اند. محدوده طرح شده در هر حالت بر روی ارتفاع 445 میلی متر تمرکز دارد.
این نسبت تکافوی احتیاجات را می کند اما لازم است که عدم تطابق 10 درصد باقیمانده از جمعیت که خارج از محدوده طراحی قرار می گیرند را نیز در نظر داشت. آیا این مسئله ناراحتی و نامطلوبی ایجاد خواهد کرد و یا عملکرد موثر سیستم انسان-ماشین آن را حل خواهد نمود؟ آیا توجهی به بهداشت و ایمنی استفاده کنندگان در کوتاه مدت و دراز مدت وجود دارد؟ شخصی که کوچکتر از صدک پنجم بوده و از صندلی نهار خوردی که بسیار بلند است استفاده می کند ممکن است در هنگام خوردن نهار یا شام کمی احساس ناراحتی کند اما اگر او نتواند پدال ترمز اتومبیل خود را به راحتی فشار دهد و یا جلو ماشین خود را ببیند, نتیجه کار بسیار نامطلوب و جدی خواهد بود. طراح بایستی در قضاوت خود این قبیل مسئل را مورد توجه قرار دهد.
در یک مفهوم کلی تر, در صورتی می توان صدک ها رو تعیین و مشخص نمود که جمعیت استفاده کننده کاملا مشخص شده باشد. وقتی طراح برای جامعه نظامیان طراحی می کند اسن مسئله بسیار ساده است, اما هنگامی که استفاده کنندگان از وسایل حمل و نقل شهری مطرح هستند قضیه کاملا متفاوت می باشد. آیا کودکان نیز بایستی همانند بزرگسالان در نظر گرفته شوند و یا سالخوردگان, زنان آبستن و معلولین؟ ممکن است این افراد به راحتی با جداول صدکهای آنتروپومتری قابل انطباق نباشند اما از طرف دیگر نبایستی حضور آنها را در جامعه و محیط نادیده گرفت. مساله طراحی بدون مانع در بخش های بعدی مورد بحث قرار می گیرد, اما در ابتدا بایستی مشکل طراحی برای اکثریت را مورد توجه قرار دهیم.
2-2 محدودیت ها و معیارها
در ارگونومی و آنتروپومتری محدودیت عبارت است از یک ویژگی قابل مشاهده و ترجیحا قابل اندازه گیری انسانی که تاثیراتی را بر روی طراحی یک مصنوع خاص ایجاد می کند. معیار عبارت است از استانداردی در قضاوت که بوسیله ان تطابق میان استفاده کننده و مصنوع سنجش می شود. بایستی درجات مختلف سلسله مراتب معیارها را تشخیص دهیم. در بالای این سلسله مراتب احتیاجاتی نظیر راحتی, ایمنی, بازدهی, زیبایی و غیره قرار دارد که آن را معیارهای برتر, عمومی یا اولیه می نامیم. به منظور دستیابی به این اهداف بایستی تعداد زیادی از معیارهای سطح پایین, ویژه یا ثانویه تامین گردند. ارتباط میان این مفاهیم را می توان به ویله مثالی روشن ساخت. در طراحی صندلی, راحتی یکی از معیارهای مشهود اولیه است, طول ساق پای استفاده کننده محدودیتی را در طراحی ایجاد می کند, زیرا اگر صندلی بلند باشد فشاری که به ناحیه خلفی ران وارد می آید موجب ناراحتی می شود. این مطلب ما را به سمت پیشنهاد معیار ثانویه هدایت می کند یعنی اینکه ارتفاع سطح نشست گاه نبایستی بلندتر از فاصله عمودی کف پا و زانو باشد ( این بعد را «ارتفاع رکبی» می خوانند).
جدول اطلاعات, توزیع این بعد را مشخص می کند. انتخاب صدک پنجم ارتفاع ارتفاع رکبی کوتاهتر است در محدوده طراحی قرار گیرد, زیرا اگر شخصی که دارای ارتفاع رکبی کوتاهتر است در محدوده طراحی قرار گیرد, 95 درصد از جمعیت که درای پا های بلندتر هستند نیز در این محدوده قرار خواهند گرفت. این مطلب کم و بیش ما را به سمت ویژگی طراحی یا معیار سوم رهنمود می سازد, ارتفاع سطح نشستگاه صندلی نبایستی بیشتر از 400 میلی متر باشد. ( توجه داشته باشید که اگر نشستگاه قابل تنظیم را پیشنهاد کنیم از این معیار به طور متفاوتی استفاده خواهیم کرد, همانند شکل 4-2 برای بحث بیشتر در این زمینه به فصل 11 رجوع کنید.)
معیار اولیه عموما در بین تعدادی از ارگونومیست ها به عنوان « نگاهی مجذوب کننده به مشهودات (SGO)» شناخته می شود. به طور کلی لازم است که قبل از هر گونه توصیه سوذمند و عملی, کلیه سطوح سلسله مراتب از بالا به پایین طی شود. بعضی از نظریه پردازان تمایل دارند گه نگارش «بالا به پایین» که در آن از معیارهای عمومی به سمت معیارهای ویژه گام برداشته می شود را در مقابل نگرش «پایین به بالا» که از معیارهای ویژه به معیارهای عمومی دست می یابد, قرار دهند.
در هر سطحی از سلسه مراتب مذکور ممکن است تفاوتهایی میان معیارها به وجود ۀید که لزوم توجه به نقطه بهینه را ضروری سازد. در مثالی که در بالا ذکر شد معیار ثانویه تنها به ما می گوید که چه موقع ارتفاع سطح نشستگاه بلند است و در مورد کوتاه بودن آن اشاره نمی کند. معیاری که سطح نشستگاه را کمتر تعریف و مشخص شده اند. از طرفی اگر مرد بلند قدی از یک صندلی که براساس صدک پنجم ارتفاع رکبی جامعه زنان طراحی شده است, استفاده کند به احتمال قوی احساس ناراحتی خواهد نمود که از این رو بایستی تمهیداتی صورت گیرد تا افراد بلند قد جامعه نیز بتوانند با حداکثر راحتی از ان استفاده کنند. به طریق مشابه, ممکن است وضعیتی وجود داشته باشد که ضرورت یابد. برای مثال بین راحتی در مقابل بازدهی یا ایمنی نقطه بهینه ای یافت شود.
در مباحث عملی, نقطه وسط سلسله مراتب, بهترین نقطه برای شروع است (شنیده ام این را به نام نگرش «وسط به خارج» خوانده اند). بنابراین این چهار دسته از محدودیت هایی را که بسیاری از مشکلات آنتروپومتری از آنها منشاء می گیرند مورد توجه قرار می دهیم و آنها را محدودیتهای اساسی آنتروپومتری می نامیم که شامل: فضای اضافی, حد دسترسی, وضعیت بدنی و قدرت می باشند.
فضاهای اضافی
در طراحی پست های کار لازم است که فضا هایی برای سر, آرنج و … در نظر گرفته شود. محیطها بایستی فضای گردش و حرکت و دسترسی را مهیا کنند. دستگیره ها می بایست فضای کافی را برای انگشتان یا کف دست فراهم آورند. تمام اینها محدودیت هایی است که فضای اضافی ایجاد می کند. اینها محدودیت های یک طرفه اند و حداقل فضای قابل قبول در یک شیء را تعیین می کنند. اگر این اندازه طوری تعیین شود که افراد چاق و بزرگ جامعه, مورد نظر قرار گیرند. (برای مثال صدک نودوپنجم طول قد, پهنا و …) بقیه افراد جامعه ضرورتا در محدوده طراحی قرار خواهند گرفت.
حد دسترسی
توانایی در گرفتن و کار کردن با کنترلهلی مثالی مشخص در این زمینه است همانند محدودیت های اشاره شده در مورد ارتفاع سطح صندلی یا امکان داشتن دید از بالای مانع حد دسترسی حداکثر فاصله قابل قبول از شی را تعیین می کند. حد دسترسی از نوع محدودیتهای یک طرفه ای می باشد با این تفاوت که در اینجا این فاصله براساس کوچیکترین فرد جامعه (صدک پنجم) تعیین می شود.
وضعیت بدنی
ارتباط میان ابعاد پست کار و اندازه های بدنی فرد که تعیین کننده وضعیت بدنی اوست سعی میکنیم که در بخش های بعدی توضیح کامل را بدهیم. ارتفاع سطح میزکار ( خواه برای حالت ایستاده و خواه برای حالت نشسته) مثال خوبی در این زمینه است. در این گونه موارد هم کوتاه بودن سطح میزکار و هم بلند ودن آن نامطلوب است بنابراین یا محدودیتی دو طرفه روبهرو هستیم که در آن کلیه افراد اعم از کوتاه قد و بلند قد در خور توجه هستند. معیارهای وضعیت بدنی اغلب اجتناب ناپذیرتر از معیارهای حدود دسترسی و فضای اضافی هستند.
قدرت
محدودیت چهارم ه مقدار قابل قبول نیرویی که در کنترل فرایند و یا دیگر وظایف بدنی و دستی بایستی اعمال شود, مربوط می شود. گاهی اوقات قدرت انسان محدودیت یک طرفه ای را تحمیل می کند و از این جهت کافی است که توانایی ضعیفترین فرد را مد نظر قرار داد. اما در بعضی موارد ممکن است این نگرش نتیجه نامطلوبی برای افرادی که دارای دستانی قوی و سنگین هستند در برداشته باشد.
3-2 گوناگونی اطلاعات آنتروپومتریکی
مرسوم است که اطلاعات آنتروپومتریکی استاتیک و دینامیک از یکدیگر تمیز داده شوند. متاسفانه این اصلاحات به طریقی که یک فیزیکدان آنها را مورد استفاده قرار می دهد, یعنی برای مشخص کردن وجود یا عدم وجود حرکت به کار نمی روند. این موضوع سبب شده که بعضی از صاحب نظران به جای دو اصطلاح فوق از واژه های «آنتروپومتری ساختاری» و «آنتروپومتریکی فونکسیونل» استفاده کنند. البته این اصطلاحات مورد تایید و پذیرش عموم نیست, بنابراین ما واژه های مرسوم یعنی استاتیک و دینامیک را به کار خواهیم برد.
اطلاعات آنتروپومتریکی استاتیکی به ابعاد و اندازه های بدن در وضعیت ساختاری ثابت مربوط می شوند که معمولا به وسیله نقاط مشخص آناتومیک در یک وضعیت مشخص اندازه گیری می شوند. برای مثال طول قد, ارتفاع چشم یا آرنج در وضعیت ایستاده یا نشسته, طول اندام ها, پهنای شانه ها یا باسن و عمق های مختلف ( اندازه های جلو, عقب) مثالهایی از ابعاد و اندازه های ایستاتیکی هستند. محیط اندامها و تنه و وزن نیز در این دسته قرار می گیرند.
اطلاعات آنتروپومتریکی دینامیکی شامل اندازه های حدود دسترسی و فضاهای اضافی می باشد که تحت شرایط عمل, اندازه گیری می شوند. منظور از شرایط عمل مثلا حالتی است که به فرد آزادی داده می شود تا برای انجام وظیفه محوله, وضعیت بدنی طبیعی به خود بگیرند. با نزدیک شدن شرایط اندازه گیری به شرایط واقعی و آنچه که در عمل وجود دارد ارتباط مستقیم و بلافاصله این گونه اطلاعات با طراحی عملی افزایش می یابد. متاسفانه, بهای چنین ارتباطی ان است که اندازه ها فقط با ویژگی های وضعیت مورد نظر وفق دارد. به همین دلیل اندازه گیری حدود دسترسی در کابین یک هواپیما ممکن است تشابهی با اندازه گیری آنها در یم اتومبیل نداشته باشد, زیرا در طراحی صندلی و تجهیزات و حتی جمعیت استفاده کننده تفاوت هایی وجود دارد. نتیجه اینکه, جمع اوری اطلاعات دینامیکی اغلب بایستی برای مسائل خاص طراحی صورت گیرد, و این هم از نظر زمان و هم از نظر پرسنل پرهزینه می باشد. در بسیاری از موارد نواقص اطلاعات استاتیکی به اندازه ای که به نظر می رسد قابل توجه نیست و این کمی و کاستیها را می توان با استفاده هوشیارانه از معیارها برطرف نمود.
نوع دیگری از اطلاعات آنتروپومتریکی وجود دارد که در اینجا فقط اشاره مختصری به آن می شود زیرا این اطلاعات ارتباطی به مسائل طراحی ندارند. این دسته شامل اطلاعاتی در زمینه ترکیب بدن نظیر ضخامت پوست (شاخصی برای مقدار چربی زیر جلدی) می باشد. به دلیل مشابه, برای حفظ ایجاز از بحث در مورد طبقه بندی فیزیک جسمی اجتناب می شود.
4-2 کارآزماییهای تطبیقی و روش حدها
حال بیایید مفاهیم ارائه شده در بالا را مورد برسی قرار دهیم و آنها را در نمونه ای از یک طراحی به کار بندیم. جزئیات مساله را احتمالا بیش از آنچه که در عمل ضرورت پیدا می کند تجزیه و تحلیل و مو شکافی می کنیم. وظیفه ما تعیین ارتفاع مناسب سطح میز کار برای یک خط مونتاژ صنعتی است که در آن کارگر بایستی دقت و قدرت متوسطی را اعمال کند. می توان فرض کرد که بنا به دلایلی کار مونتاژ به صورت ایستاده, و نه نشسته, انجام می گیرد . همین طور نیروی کار ما نماینده ای از جمعیت مردان بزرگسال است. چگونه بایستی آغاز کرد؟
یکی از طرق بسیار خوب رها کردن تئوری و پرداختن به نگرش تجربی انجام کارآزمایی تطبیفی است. برای این منظور به سطحی نیاز داریم که ارتفاع آن قابل تنظیم است و عمل مونتاژ (یا هر فعالیت مشابه دیگر) بر روی ان انجام می گیرد و همین طور به نمونه ای از افراد که نماینده جمعیت استفاده کننده هستند. هر فرد, مونتاژ را بر روی سطح میز کار با ارتفاعات مختلف انجام می دهد و سپس در مورد ارتفاع سطح میز کار به صورت «خیلی بلند», «خیلی کوتاه» و مناسب قضاوت می کند. برای تعدیل قضاوتهای صورت گرفته می توان از مقادیر واسطه استفاده نمود. قطعا بایستی احتیاطهایی در مورد تورش قضاوت هایی افراد انجام داد. برای مثال ترتیبی که ارتفاع میز کار تغییر می کند یا به عبارتی ارتفاع های مختلف به کارگر عرضه می شود بایستی با توجه به مطلب ذکر شده برنامه ریزی شود. کارآزمایی تطبیقی عمدتا یک آزمایش فیزیکی-روانی است که در آن افراد در مورد احساسی (نظیر راحتی) که ناشی از واکنش در برابر محرک فیزیکی خاصی است (نظیر ارتفاع میز کار), قضاوت می کنند. استفاده از روش های فیزیکی- روانی در مطالعات ارگونومی به وسیله چاپانیز (1959), پپرمنز و کارلت (1983) به بحث گذاشته شده و کارآزمایی تطبیقی به وسیله جونز (1966, 1963) مورد بحث قرار گرفته است. بعد از انجام کارآزماییهای تطبیقی اطلاعاتی در اختیار خواهیم داشت که مارا قادر می سازد تا درصدی از استفاده کننده گان را که در یک ارتفاع معین با راحتی کار می کنند, تخمین زنیم. اطلاعات نه تنها بازگوکننده تنوع انتروپومتریکی افراد است بلکه منعکس کننده توانایی انها در قضاوت در مورد مناسبترین وضعیت کاری نیز می باشد.
آیا بایستی برای هر طراحی, چنین کارآزمایی تطبیقی سیستماتیکیرا انجام داد؟ چنین خط مشی بنا به دلایل مالی و پرسنلی (بجز در موارد استثناء) غیر عملی است و از آنجا که می توانیم به وسیله تجزیه و تحلیلی که با قلم و کاغذ انجام می گیرد به نتایج مشابه دست یابیم, لذا در بسیاری از موارد استفاده از روش کار آزمایی تطبیقی ضرورتی ندارد. ممکن است این قبیل تکنیک ها را بعنوان مدل یا مشابه کارآزمایی تطبیقی مورد توجه قرار دهیم, که در آنها اطلاعات معیارهای آنتروپومتریکی برای بیان افراد واقعی مورد استفاده قرار می گیرند.
گراند جان (1981) بهترین ارتفاع میز کار را برای کارهای دستی که احتیاج به دقت و قدرت متوسط دارند, 50 تا 100 میلی متر درزیر ارتفاع آرنج توصیه می کند که این مقدار معیار ما خواهد بود. همانطور که ملاحظه می شود این معیار یک معیار دو طرفه است زیرا از هر طرف امکان افزایش دارد. «ارتفاع آرنج» (EH) در مردان انگلیسی برابر با [52] 1090 میلی متر است (رجوع کنید به جدول 1-4). برای در نظر گرفتن کفش ها 25 میلیمتر به مقدار آن اضافه می شود و در نتیجه عدد [52] 1115 میلی متر به دست می آید(رجوع کنید به جدول 2-4), تلفیق این اطلاعات با معیار فوق حد بالایی و حد پایینی ارتفاع بهینه میز کار را به دست می دهد.
میلی متر [EH-50=1065 [52 , میلی متر [EH-100=1015[52
این اطلاعات را می توان به عنوان ابعاد آنتروپومتریکی که دارای توزیع طبیعی هستند به کار گرفت و صدکها را در این توزیع محاسبه نمود. البته بایستی توجه نمود که این معیار مربوط به ارتفاع بهینه میز کار است. از آنجا که می توانیم به طور معقول فرض کنیم که افراد آمادگی پذیرفتن شرایط کمتر از حد کمال را دارا هستند. بنابراین می توان دو ناحیه دیگر, یعنی 50 میلی متر در بالا و پایین ارتفاع بهینه, را پیشنهاد نمود که به عنوان نواحی مناسب و قابل قبول و نه در حد کمال مشخص می شوند (رجوع کنید به شکل 5-2).
شکل 5-2: معیار ارتفاع بهینه و مناسب میز کار در عملیات مونتاژ صنعتی
جدول 2-2 مجاسبات کاملی را که بر روی ارتفاع 1000 میلی متر انجام گرفته نشان می دهد. این مقدار معادل صدک هفتادوپنجم کوچکترین معیار است (EH-150mm), بنابراین چنین استنتاج می شود که ارتفاع 1000 میلی متر برای 25% از مردانی که بلندتر از آن هستند بسیار کوتاه یا نامناسب است. به طریق مشابه دو معیار وسطی (EH-100mm و EH-50mm) به ترتیب برابر با صدک های سی و نهم و یازدهم است و چنین نتیجه میشو که 28% از افرادی که بین دو ارتفاع قرار دارند ارتفاع میز را بسیار مناسب یا بهینه خواهند یافت.
جدول 2-2: محاسبه درصد مردانی که با انتخاب میزی با ارتفاع 1000 میلی متر در محدوده طراحی قرار می گیرند.
|
معیار |
توزیع |
صدک |
نتیجه گیری |
|
EH-150 |
965/52/ |
75 |
بسیار کوتاه – 25% |
|
EH-100 |
1015/52/ |
39 |
کوتاه – 61% |
|
EH-50 |
1065/52/ |
11 |
بلند – 11% |
|
EH |
1115/52/ |
1 |
بسیار بلند – 1% |
|
مناسب – 28% |
|||
می توان انجام چنین محاسباتی را تا دست یافتن به ارتفاعی که بین حداکثر افراد بهینه باشد ادامه داد(البته برای این منظور می توان از کامپیوتر بهره گرفت). در اینجا حالت شخصی را داریم که با طرز تفکر آماری به دنبال بهترین شرایط می گردد. نتایج مربوط به یکسری از محاسبات فوق الاشاره در شکل 6-2 رسم شده است. تعجبی ندارد که حالت بهینه, منحنی توزیع طبیعی را توصیف کند (e) در حالی که حالتهای بلند و کوتاه منحنی نرمال اُجیوه را که در جهت مخالف روبروی یکدیگر قرار دارند, تداعی می کند (a,b,c,d). ممکن است بهینه را با کمی کوتاه و کمی بلند در هم اردغام کرده و حالت «مناسب» را ایجاد کنیم (f) و بقیه را که خارج از این محدوده قرار می گیرند تحت عنوان نامناسب طبقه بندی نماییم (g)؛ (26% نامناسب و 74% مناسب برای ارتفاع 1000 میلی متر). با توجه به توضیحات ارائه شده, منطقی است که ارتفاع 1050 میلی متر را انتخاب کنیم.
اما این پایان مساله نیست زیرا حدود 15 درصد از استفاده کنندگان در خارج از محدوده طراحی قرار گرفته و دارای تطابق نامناسب می باشند. آیا این حالت, وضعیتی قابل قبول یا قابل تحمل می باشد و یا شدیدا ناراحت کننده بوده و موجب بروز عوارض سوء در دراز مدت می شود؟ یا بهتر است سطح میزکار بلندتر باشد یا کوتاه تر؟ آیا حقیقتا به میز کاری که ارتفاع آن قابل تنظیم است و یا راه حل های مشابه دیگر احتیاج داریم؟
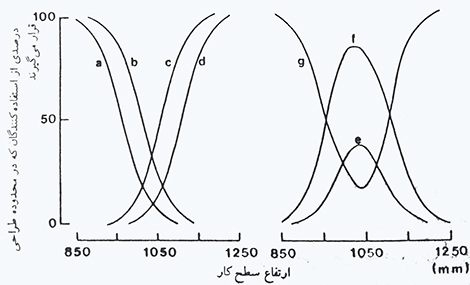
روش انتروپومتری حدها که در تعیین ارتفاع بهینه میز کار به کار رفته است. منحنی ها نشان هنده درصد استفاده کننده هایی است که در محدوده طراحی قرار گرفته و یا قرار نمی گیرند: (a) بسیار کوتاه, (b) کوتاه, (c) بلند, (d) بسیار بلند, (e) راضی کننده, (f) مناسب, (g) نامناسب. برای تعریف گروهها و بحث در مورد روش به متن مراجعه شود
شکل 6-2: روش انتروپومتری حدها که در تعیین ارتفاع بهینه میز کار به کار رفته است. منحنی ها نشان هنده درصد استفاده کننده هایی است که در محدوده طراحی قرار گرفته و یا قرار نمی گیرند: (a) بسیار کوتاه, (b) کوتاه, (c) بلند, (d) بسیار بلند, (e) راضی کننده, (f) مناسب, (g) نامناسب. برای تعریف گروهها و بحث در مورد روش به متن مراجعه شود.
فرایندی که برای حصول بهترین نتیجه و راه حل مورد استفاده قرار می دهیم گاهی بعنوان روش حدها خوانده می شود. این نام که از یک تکنیک آزمایشی در روان شناسی گرفته شده و از نظر شکل بسیار شبیه ان است, تایید می کند که این فرایند یک کارازمایی تطبیقی خیالی است.
5-2 گوناگونی در شکل و تناسب بدنی
در آزمایش های متداول, انسانهازمانی کهاز نظر سن, جنس و نژاد به یک جمعیت همگن تعلق داشته باشند,از نظر شکل و ابعاد بدن بسیار متنوع و گوناگون می باشند. اگر می خواستیم نمونه ای از مردان با طول قد یکسان را انتخاب کنیم بایستی انتظار می داشتیم که نسبتهای بدنی گوناگونی روبرو شویم نتایج عملی چنین مشاهدات مقدماتی بسیار قابل توجه است.
متخصصان علم انسان شناسی به طور مرسوم در پی تعریف نسبتهایی بوده اند که در آنها نسبت یک بعد در مقایسه با بعد دیگر مطرح می شود. معمولا این نسبت ها را «شاخصهای درصدی» می نامند, از این رو:
این شاخص توصیفی است که برای تک تک افراد مطرح است و بنابراین در میان جمعیت توزیعی دارد که می توان میانگین و انحراف معیار آن را از طریق معمول محاسبه نمود. در مطالعه جامعی که بر روی افراد غیرنظامی آمریکا صورت گرفت (استوت و همکاران 1965, 1970) شاخص فوق الذکر برای مردان و زنان به ترتیب [1/5]51/8 و [1/5]52/4 بدست آمد ( اما توزیع آن دارای چولگی مختصری بود). توزیع شاخص ارتفاع نشسته می بایست از روی اطلاعات خام محاسبه شود (مگر اینکه از تکنیکهای بسیار پیشرفته آماری استفاده کنیم). اگر اطلاعات خام در دسترس نباشد (که معمولا چنین است) به عنوان جایگزین می توان از بعد نسبی استفاده کرد. بنابراین:
 بنا به دلایلی که برای دانشمندان علم امار و ریاضی مشخص است میانگین (x/y) برابر با میانگین x/y نمی باشد. بنابراین ارتفاع نشسته نسبی تخمین یا تقریبی از میانگین شاخص ارتفاع نشسته است. (اصلاحاتی را که در اینجا تعریف کردیم گاهی اوقات معادل یگدیگر تلقی می شوند.)
بنا به دلایلی که برای دانشمندان علم امار و ریاضی مشخص است میانگین (x/y) برابر با میانگین x/y نمی باشد. بنابراین ارتفاع نشسته نسبی تخمین یا تقریبی از میانگین شاخص ارتفاع نشسته است. (اصلاحاتی را که در اینجا تعریف کردیم گاهی اوقات معادل یگدیگر تلقی می شوند.)
طریق دیگر بررسی دو متغیر, که از نظر اماری پیچیده تر است,استفاده از تکنیک های رگرسیون و همبستگی و با توجه به مفهموم توزیع طبیعی دو گانه می باشد. محاسبات ریاضی این تکنیکها در کلیه کتاب های آمار وجود دارد. در اینجا موضوع را دید کیفی مورد توجه قرار می دهیم. دو متغیر را با توزیع طبیعی در نظر بگیرید, مثلا پهنای شانه و طول قد. میزان ارتباط یا وابستگی بین متغیرها را می توان به وسیله پارامتری به نام ضریب همبستگی (r) بیان نمود. اگر دو متغیر هیچ گونه ارتباطی با یکدیگر نداشته باشند r برابر صفر خواهد بود, اگر دو متغیر ارتباطی کامل با یکدیگر داشته باشند r برابر با 1+ یا 1- خواهد بود (1+ ارتباط مستقیم, 1- ارتباط معکوس). توزیع طبیعی دوگانه بوسیله میانگین انحراف معیار دو متغیر مورد نظر و ضریب همبستگی بین آنها به طور کامل تعریف می شود. تابع احتمال یک توزیع دو گانه, به صورت منحنی سه بعدی می باشد. به جای رسم این سطوح, آسانتر این است که آنها را به صورت «نقشه های کنتورکشی شده» نمایش دهیم که در آنها هر خط گویای احتمال برابر است (شکل 7-2). وقتی متغیر X و Y غیر وابسته هستند (r=0), خطوط هم احتمال, به صورت دایره های هم مرکز می باشند. با افزایش r این شکل رفته رفته پهن شده و به صورت بیضی در می آید. وقتی که متغیرها به طور کامل به یکدیگر وابسته باشند (r=1), سطح بیضی تبدیل به یک خط مستقیم می شود.
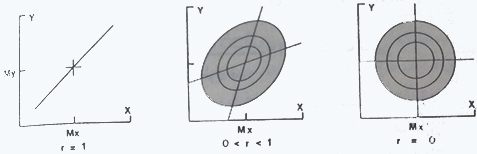
خطوط هم احتمال در توزیع طبیعی دو گانه که دارای درجات مختلف همبستگی هستند.Mx,My مقادیر میانگین متغیرهای x و y می باشند
شکل 7-2: خطوط هم احتمال در توزیع طبیعی دو گانه که دارای درجات مختلف همبستگی هستند.Mx ,My مقادیر میانگین متغیرهای x و y می باشند.
آنها همبستگی شدیدی ملاحظه می شود. از طرف دیگر شانش مواجهه با شخصی که در تعدادی از ابعاد آنتروپومتریکی «متوسط» باشد بسیار کم است. اما قبل از اینکه به این نتیجه گیری عجولانه برسیم که «شخص متوسط وجود ندارد» بایستی به این نکته توجه کنیم که شخص متوسط هنوز محتمل ترین عضو یک جمعیت است. در پاراگراف قبل یک توزیع طبیعی دو گانه توضیح داده شد. تصور یا تجسم کردن یک توزیع چندگانه دشوارتر خواهد بود زیرا تابع احتمال ان را منحصرا می توان در فضای چهار بعدی رسم نمود. از طرف دیگر این تابع هنگامی ماکزیمم است که تمام ابعاد در حد متوسط خود باشند.
مهمتر اینکه, از نظر ریاضی غیر ممکن است که فردی را در نظر بگیرید که در طول تنه و طول پایین تنه برابر با صدک نود و پنجم باشد, نتیجه حاصل ضرورتا بایستی بزرگتر از صدک نودوپنجم طول قد باشد, زیرا در افراد بلند قد بعضی دارای پاهای بلند نامتناسب و بعضیی دارای تنه بلند نامتناسب هستند. ( از انجا که انسانها دارای اشکال متفاوت می باشند همبستگی بین طول تنه یا طول پا و قد کمتر از یک می باشد) روش های طراحی که در آنها صدک نود وپنجم یا صدک پنج مورد نظر قرار می گیرند, برپایه قراردادهای ساده ای استوار هستند. متاسفانه روشهای جایگزین یا روشهایی که از نظر ریاضی پیشرفته تر هستند ممکن است بسیار پیچیده باشند. در مجموع کافی است که طراح از محدودیتهای فرضیات ساده صدک مطلع بوده و اطمینان پیدا کند که این فرضیات او را به سوی ارتکاب اشتباه عمده نمی کشاند.
یکی پست کار نظیر کنسول کنترل را در نظر بگیرید که طراحی ان چندین بعد آنتروپومتریکی در نظر گرفته شده است ( ارتفاع زانو, ارتفاع آرنج نشسته, ارتفاع چشم نشسته و …) و برای هر بعد صدک ها طوری انتخاب شده اند که 95 درصد افراد جامعه در محدوده طراحی قرار گیرند. حال سوال این است که در پایان کار چه درصدی از جمعیت استفاده کننده در محدوده طراحی قرار خواهند گرفت؟
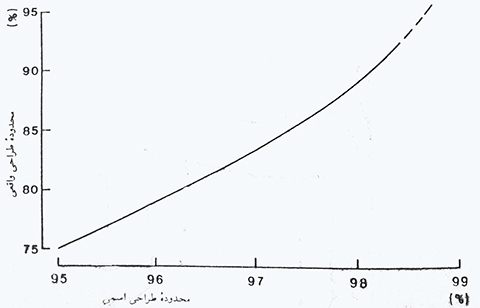
هر بعد 5 درصد از افراد را از محدوده طراحی خارج نموده است, اما به علت اینکه ابعاد به طور کامل با یکدیگر وابسته نیستند در هر نوبت بیش از 5 درصد از افراد در خارج از محدوده طراحی قرار می گیرند. در اصل, این بیرون افتادگی می توانست تا حد هشدار دهنده ای برسد! بیتنر و همکان (1975) مساله را بوسیله یک تکنیک کامپیوتری به نام «مدل سازی مونت کارلو» مورد مطالعه قرار دادند. در اصل, کامپیوتر رسته ای اعداد تصادفی ایجاد می کند که دارای توزیع طبیعی چندگانه مشابه با اطلاعات آنتروپومتریکی افراد می باشد. (در اینجا احتیاجی نیست که بحث پیرامون چگونگی دستیابی به این شاهکار برجسته بپردازیم). نتیجه محاسبات در شکل 8-2 نمایش داده شده است. محدوده طراحی مورد نظر (اسمی) در محور افقی قرار دارد. درصد واقعی افرادی که با در نظر گرفتن هفت محدودیت جداگانه آنتروپومتریکی در محدوده ی طراحی قرار گرفته اند به طور عمودی ترسیم شده است. با توجه به شکل می توان به این حقیقت هوشیارکننده دست یافت که هنگامی که قرار گرفتن 95% از جمعیت در محدوده طراحی مورد نظر باشد, آنچه که در عمل حاصل خواهد شد بیرون افتادن 25% افراد از محدوده طراحی است (یعنی تنها 75% جمعیت در محدوده طراحی قرار می گیرند).
شکل 8-2: محدوده طراحی اسمی و واقعی در طراحی پست کار که در ان هفت بعد دخالت داشته اند. محاسبات بوسیله «مدلسازی مونت کارلو» صورت گرفته است. اطلاعات از بیتنر و همکاران (1975) برگرفته شده است.
2-6 انسان نماها, مدل ها و کامپیوترها
از انجا که بسیاری از ما دنیای محدود جداول آماری را خسته کننده می یابیم, لذا ضروری است که اطلاعات آنتروپومتریکی به صورت فشرده تر درآید, به شکلی که به راحتی و به سرعت قابل استفاده باشد؛ در حقیقت مدلی از اطلاعات که به راحتی در اختیار بوده و نتیجه تصمیمات طراحی در صورت امکان نه سرعت بوسیله حس بینایی ارزیابی شود. ساده ترین این مدلها شکل دو بعدی انسان نما است که تقریبا شبیه بدن انسان می باشد.
2-9: مدل انسان نما, زنی با صدک پنجم (مقیاس 0.1)
ذکر این مطلب مهم است که بنا به دلایل ذکر شده در بخش قبل وجود انسان نما با صدک نودوپنجم, حداقل در تئوری غیرممکن است به توافقی دست یابیم که در ان اکثر ابعاد بحرانی مورد توجه قرار گرفته باشند. انسان نمادهایی که اشکال 9-2 تا 12-2 ملاحظه می شود براساس اطلاعات حاضر )رسم شده اند و عقیده دارم که این اشکال برای مقاصد عملی دارای دقت و صحت کافی می باشند. (صدکهای مختلفی از انسان نماها را می توان از شرکت CCD تهیه نمود.)
شکل 10-2 مدل انسان نما, زنی با صدک 95 (مقیاس 0.1)
به نظر می رسد که اینده, پیشرفت های عمده ای را در مدل سازی کامپیوتری داده های انتروپومتریکی شاهد خواهد بود. برنامه کامپیوتری «سامی» که به وسیله پروفسور موریس بانی و همکارانش تکمیل شد, یکی از مثال های خوب در این مورد است. در واقع کامپیوتر مقدار زیادی از جداول آنتروپومتریکی را در خود ذخیره می کند و تصویری سه بعدی از استفاده کننده به دست می دهد که دارای صدک مشخصی است. سپس این تصویر بر روی صفحه مانیتور به صورت نما, پلان, طرح یا پرسپکتیو نمایش داده می شود. همچنین حرکت ان به اطراف تحت کنترل اپراتور امکان پذیر است.
شکل 11-2: مدل انسان نما, مردی با صدک پنجم (مقیاس 0.1)
بدین ترتیب طراحی انجام شده از نظر حدود دسترسی, تناسب, فضای اضافی و میدان دید و قابل ارزیابی خواهد بود. از این سیستم کامپیوتری می توان بعنوان ابزار طراحی و ارزیابی استفاده نمود و تا کنون نیز برای طراحی وسایل نقلیه (کامیونها, اتومیبل ها, تراکتورها, کشتی ها, هواپیماها و قطارها) و سایر وسایل و تجهیزات نظیر طراحی فضای پرداخت پول در فروشگاهها و طراحی تجهیزات کامپیوتری و جانمایی اتاقهای کنترل مورد استفاده واقع شده است. شکل 13-2 یک کاربرد غیر متداول از این سیستم را نشان می دهد. در این شکل مدل انسان نمای یک زن بلند قد (یک پرستار) نمایش داده شده است. برای طراحی تختخواب که درای طراحی ویژه میباشد خم شده است. برای طراحی تختخواب مورد نظر با توجه به دو معیار راحتی و سهولت استفاده, ابعاد مختلفی مورد آزمایش قرار گرفت. توصیه هایی که براساس ارزیابی با سیستم سامی ارائه شده قبل از انجام آزمایش بر روی استفاده کننده به صورت بازخورد به طراح منتقل گردید. (این پروژه توسط استوارت گیبسون و ایان پمبرتون انجام پذیرفت.)
برنامه مشابه دیگیری که همانند مدل مونت کارلو عمل می کند به نام CAPE شناخته می شود که توسط بیتنر و همکاران (1975) ارائه شده است.
پیشگویی تاثی در دسترس بودن فزاینده چنین نرم افزارهایی در طراحی و آنتروپومتری مشکل است. تصور کنید که یک بسته سامی همراه با سیستم CAPE که خود همانند کارشناس یا یک سیستم هوشمند عمل می کند در طراحی و تولید گرافها و اشکال گرافیکی به کار گرفته شوند. چنین سیستمی یک ابزار قوی طراحی را تشکیل خواهد داد.
این مطلب بروزرسانی شد و فایل اصول آنتروپومتری مهندس سنجری در 9 صفحه پیوست شد.
ورود یا ثبـــت نــــام + فعال کردن اکانت VIP
مزایای اشتراک ویژه : دسترسی به آرشیو هزاران مقالات تخصصی، درخواست مقالات فارسی و انگلیسی، مشاوره رایگان، تخفیف ویژه محصولات سایت و ...
حتما بخوانید:
⇐ آنتروپومتری و کاربرد آن در طراحی


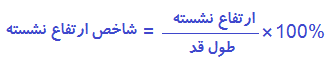



دیدگاهتان را بنویسید
می خواهید در گفت و گو شرکت کنید؟خیالتان راحت باشد :)