ابزارهای ریاضی برای بروزرسانی احتمالات در ریسک

ابزارهای ریاضی برای بروزرسانی احتمالات در ریسک

فرمت: Pdf  تعداد صفحات: 24

فهرست:

• بروزرسانی با بیزین
  • نمادها و اصطلاحات مورد استفاده در بروزرسانی بیزین
  • قضیه ی بیز
  • نظریه فراوانی گرایانه در مقابل نظریه بیزین
  • نظریه احتمال فراوانی گرایانه
  • نظریه بیزین
  • گام های اجرایی برای تجزیه و تحلیل بیزین.
  • مثال: نقص در باز شدن شیر
  • مثال: نقص در کارکرد پمپ
  • نتیجه گیری
• تجزیه و تحلیل مونته کارلو
  • مثال: توزیع عادی
  • مثال: تصمیم گیری سوئیچ
• خودآزمایی
• منابع

مقدمه

در این بخش به دو ابزار رایج که برای بروزرسانی و کمک به تعیین احتمال شکست استفاده می شود پرداخته خواهد شد. این موارد وابسته به ابزار بیزین (بروزرسانی بیزین در این روش بیزین علاوه بر مشاهدات، اطلاعات و باورهای اولیه محقق نیز مهم است و در حل مسئله نتیجه گیری مد نظر قرار می گیرند) و تحلیل مونت کارلو است. این دو تکنیک به طور گسترده در ارزیابی ریسک احتمالی (PRA) و همچنین دستکاری داده های بسیار ساده ریاضی تا الگوریتم های بسیار پیچیده استفاده شود. این بخش بر نسخه های نسبتاً ساده ی این تکنیک ها متمرکز می خواهد بود. روش های پیچیده تر را در منابع ارائه شده می توان یافت.

بروزرسانی با بیزین

در این بخش بیشتر به بروزرسانی بیزین و چگونگی استفاده از آن در PRA برای کمک به احتمالات بحث خواهد شد.

نمادها و اصطلاحات

∩- این نماد نشانگر اشتراک دو مجموعه بوده و به این معنی است که دو پیش آمد احتمالی با هم اتفاق می افتد به عنوان مثال (A∩B) احتمال این است که A و B با هم اتفاق میافتند یا با هم اشتراک دارند، اگر پیش آمدها دو به دو ناسازگار باشند، پس 0 = (A∩B)P است.

∪- این نماد اجتماع است.

احتمال وقوع پیش آمد A یا B برابر با احتمال اجتماع حوادث A و B با (P(A∪B نشان داده می شود.

(A | B)P این عبارت بیانگر احتمال وقوع پیش آمد A، به شرط اینکه پیش آمد B رخ داده باشد است احتمال شرطی نامیده می شود. احتمال شرطی پیش آمد A، با توجه به پیش آمد B، با نماد (A | B)P نشان داده می شود.

• علامت ∑ بیانگر جمع است.
• علامت به معنی حاصل همه ی مقادیر موجود در محدوده است. برای مثال:

_N=1⁴∏ 3n = 3 × 6 × 9 × 12 = 1944

 قضیه ی بیز

قضیه یا قانون بیز بیش از ۲۵۰ سال پیش توسط کشیش توماس بیز ایجاد شده است. این قضیه توسط پیر سیمون لاپلاس بروزرسانی شده و در سال ۱۸۱۲ منتشر شد. پیش فرض اصلی قضیه بیز احتمال یک پیش آمد را توصیف می کند که مبتنی بر اطلاعات قبلی در مورد شرایط مربوط به پیش آمد است. به عنوان مثال با استفاده از رویکرد بیز، احتمال وجود بیماری خاصی در یک گروه یا برای یک فرد با دانستن ویژگی هایی مانند سن، وزن و خاستگاه قومی را می توان بهتر پیش بینی کرد.

از نظر ریاضی، قضیه بیز به شرح زیر است:

P(A|B) = ^P(B|A)×P(A) / _P(B)

که در آن A و B پیش آمدها هستند و 0 ≠P(B) می باشد. و P(A|B) یک احتمال شرطی است و به معنی احتمال وقوع A به شرط وقوع B . و (BA) نیز یک احتمال شرطی است و به معنی احتمال وقوع پیش آمد B به شرط وقوع A است. P(A) و P(B) شانس یا احتمال مشاهده A و B به طور مستقل از یکدیگر یا احتمال حاشیه ای هستند.

به عنوان مثال جمعیتی از افراد را در نظر بگیرید که ممکن است داروی خاصی مصرف کنند یا نکنند. اگر افراد این دارو را مصرف کنند، ۸۰٪ احتمال دارد که یک آزمایش نتایج مثبتی را ارائه دهد. اگر استفاده نکنند %۹۹ احتمال دارد که نتایج آزمون منفی باشد مشخص شده است که ۱۰٪ از مردم از این دارو استفاده می کنند احتمال اینکه فردی که به طور تصادفی انتخاب شده و دارای تست دارویی مثبت از این دارو استفاده کند چیست؟ از این رو عبارت PU به معنای این است که افراد از دارو استفاده می کند و NU یعنی از دارو استفاده نمی کنند. در نتیجه خواهیم داشت:

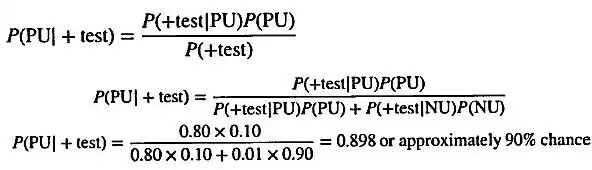
به این دلیل است که در جامعه تعداد زیادی مصرف کننده مواد مخدر وجود دارد و این احتمال وجود دارد فردی که برای آزمایش انتخاب شده، و از این دارو استفاده کند نتیجه ی آزمایش او مثبت باشد حتی اگر آزمایش اختصاصی نباشد تعداد مصرف کنندگان در یک جمعیت ۱۰۰۰ نفره، ۱۰۰ نفر است. در سناریوی دوم اگر معکوس اعداد قبل را داشته باشیم بطوریکه جمعیت مصرف کننده کوچک باشد (۰/۱%) میزان نتیجه مثبت کاذب در گروهی که مصرف کننده نبودند %۱ باشد و این آزمایش نیز اختصاصی نباشد (۸۰%) نتایج بصورت زیر خواهد بود:

P(PU| + test)= ^0.8×0.001 / _{0.8×0.001 + 0.01×0.999}

نمودارهای درختی منطقی، برای دو وضعیت محتمل (سناریوی ۱ و سناریوی ۲) در شکل ۱ و ۲ نشان داده شده است مثال های قضیه ی بیز می توانند بسیار پیچیده تر باشند در ادامه مثالی از کاربرد قضیه بیز در یک صنعت شیمیایی ارائه می گردد. یک تولید کننده مواد شیمیایی با چهار خط تولید را فرض کنید کل ظرفیت روزانه تولید محصول در کارخانه ۲۰۰۰۰۰ گالن است خط A قدیمی تر است و ۴۰۰۰۰ گالن تولید می کند. خط B بزرگترین تولید کننده است و ۶۰۰۰۰ گالن تولید می کند خطوط C و D هر کدام ۵۰۰۰۰ گالن تولید می کنند؛ این در حالی است که کیفیت محصولات در این خطوط با هم متفاوت است خط A کمترین سطح کیفیت را با ۵ مواد رده خارج را دارد؛ خط B با ۳ در رتبه بعدی و خطوط C و D به ترتیب با تولید سطح کیفیت ۱ و ۰.۵٪ از مواد رده خارج بهترین محصول را تولید می کنند.

ادامه مطلب را با دانلود فایل پیوستی مشاهده کنید.

حتما بخوانید:

⇐ مبانی احتمالات و آمار در ارزیابی ریسک

⇐ درک ریسک

⇐ ریسک ها و پیامدها